Codeforces Round #765 (Div. 2)题解

传送门：Codeforces Round #765 (Div. 2)

A. Ancient Civilization

题意：定义d(x,y)d(x, y)为二进制下xx和yy的不同位个数，现在给了nn个数，要找到一个xx使得∑i=1rd(x,a[i])\sum_{i=1}^{r}d(x, a[i])最小。

思路：通过贪心枚举每一位，假如当前这一位11的个数比00多，那么我将让xx这一位为11，否则为00。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <bits/stdc++.h>
using namespace std;

int main() {
  ios::sync_with_stdio(false);
  cin.tie(nullptr);
  int T;
  cin >> T;
  while (T--) {
    int n, m;
    cin >> n >> m;
    vector<int> a(n);
    for (auto& v : a) {
      cin >> v;
    }
    int ans = 0;
    for (int i = 0; i < 31; i++) {
      int cnt = 0;
      for (auto& v : a) {
        cnt += ((v >> i) & 1);
      }
      if (cnt * 2 >= n) {
        ans |= (1 << i);
      }
    }
    cout << ans << "\n";
  }
  return 0;
}

B. Elementary Particles

题意：找到最长的，任意两个长度相同，位置不同的连续子序列，要求这两个子序列相对位置上至少有一个值相同。

思路：我们保存每一个数的与它相同的前一个数的位置为pos[x]pos[x]，对于这样的两个序列来讲，他们的前缀长为pos[x]pos[x]，后缀长为n−in - i，答案为两者的和，每次遍历取最大即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <bits/stdc++.h>
using namespace std;
 
int main() {
  ios::sync_with_stdio(false);
  cin.tie(nullptr);
  int T;
  cin >> T;
  while (T--) {
    int n;
    cin >> n;
    vector<int> pos(150001, -1);
    int ans = -1;
    for (int i = 0; i < n; i++) {
      int x;
      cin >> x;
      if (pos[x] == -1) {
        pos[x] = i;
      } else {
        if (pos[x] + n - i < n) {
          ans = max(ans, pos[x] + n - i);
        }
        pos[x] = i;
      }
    }
    cout << ans << "\n";
  }
  return 0;
}

C. Road Optimization

题意：有一条路，路上有几个限速区间，每个区间的限速不同，通过去一个区间的代价是该区间长度*限速，有一辆小车从00开到ll，假如最多能去掉kk个限速区间，求小车行驶完整个区间的最小代价。

思路：题目给的nn只有500500，所以可以考虑O(n3)O(n^3)的dp。为了更方便处理下标，我们可以将整个区间反过来进行dp，我们用dp[i][j]dp[i][j]表示前ii个限速牌种刚好有jj个有效的最小值，此时有dp方程dp[i][j]=min(dp[i][j],dp[k][j−1]+a[i]∗(d[k]−d[i]))dp[i][j] = min(dp[i][j], dp[k][j - 1] + a[i]*(d[k] - d[i]))，方程中的kk表示ii之前的每个限速牌。最后答案取dp[n]dp[n]中第二维大于等于n−kn - k的最小值。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <bits/stdc++.h>
using namespace std;
 
const int MAX = 505;
int d[MAX], a[MAX];
long long dp[MAX][MAX];
 
int main() {
  ios::sync_with_stdio(false);
  cin.tie(nullptr);
  int n, l, kk;
  cin >> n >> l >> kk;
  memset(dp, 0x3f, sizeof(dp));
  for (int i = 1; i <= n; i++) {
    cin >> d[i];
  }
  for (int i = 1; i <= n; i++) {
    cin >> a[i];
  }
  reverse(d + 1, d + n + 1);
  reverse(a + 1, a + n + 1);
  d[0] = l;
  dp[0][0] = 0;
  for (int i = 1; i <= n; i++) {
    for (int j = i - 1; j >= 0; j--) {
      for (int k = 1; k <= j + 1; k++) {
        dp[i][k] = min(dp[i][k], dp[j][k - 1] + (long long) a[i] * (d[j] - d[i]));
      }
    }
  }
  long long ans = LLONG_MAX;
  for (int i = n - kk; i <= n; i++) {
    ans = min(ans, dp[n][i]);
  }
  cout << ans << "\n";
  return 0;
}

E1. Cats on the Upgrade (easy version)

题意：有一个括号序列，每次会询问一个区间，计算该区间有多少个连续子序列是合法的括号序列，且题目保证了给的区间一定是合法的括号序列。

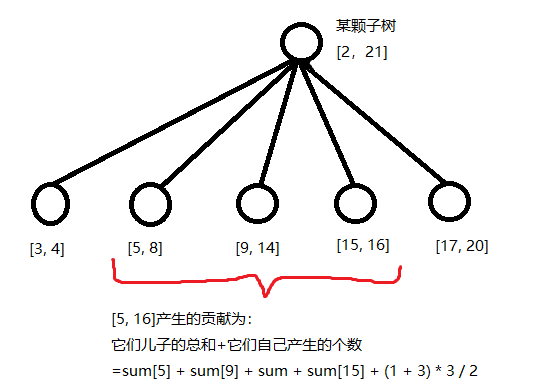
思路：因为对于一个括号序列来讲，一个左括号只会对应一个右括号，我们可以将括号序列转成一颗树，每个左括号定义为一个节点，前提是他有一个对应的右括号。对于一棵子树来说，假设这颗子树有xx个儿子，那么它儿子所构成的连续括号序列个数为(1+x)x2\frac{(1+x)x}{2}。如果现在有一个询问区间为[l,r][l, r]，假如该节点是根节点，那么它的答案就是sum[u]+1sum[u]+1，之所以+1+1是因为它自己的括号还没算进去；否则，如果不是根节点，也就是说该区间是在某个合法区间内的区间，那么我们计算出它们所有儿子的总和为∑i=lrsum[i]\sum_{i=l}^{r}sum[i]，然后计算他们自身产生的贡献，与计算儿子的贡献方式一样，只需要数出，在树的同一层，它们之间有多少个节点。

001

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <bits/stdc++.h>
using namespace std;

int main() {
  ios::sync_with_stdio(false);
  cin.tie(nullptr);
  int n, q;
  string s;
  cin >> n >> q >> s;
  stack<int> stk;
  vector<int> match(n, -1);
  for (int i = 0; i < n; i++) {
    if (s[i] == '(') {
      stk.push(i);
    } else if (!stk.empty()) {
      int p = stk.top();
      stk.pop();
      // 保存每一对匹配的括号位置
      match[i] = p;
      match[p] = i; 
    }
  }
  vector<vector<int>> edges(n + 1);
  // 通过递归创建树
  function<void(int, int)> create = [&] (int l, int r) {
    for (int i = l + 1; i < r; i++) {
      edges[l].push_back(i);
      create(i, match[i]);
      i = match[i];
    }
  };
  for (int i = 0; i < n; i++) {
    if (match[i] == -1) {
      continue;
    }
    edges[n].push_back(i);
    create(i, match[i]);
    i = match[i];
  }
  vector<int> fa(n + 1, -1);
  vector<long long> cnt(n + 1), sum(n + 1);
  // sum保存每个节点不包括他自己,只计算它儿子能形成多少个有效括号序列: (1 + x) * x / 2
  function<void(int)> dfs = [&] (int u) {
    int x = int(edges[u].size());
    cnt[u] = (long long) (1 + x) * x / 2;
    for (auto& v : edges[u]) {
      fa[v] = u;
      dfs(v);
    }
  };
  dfs(n);
  sum[0] = cnt[0];
  for (int i = 1; i <= n; i++) {
    sum[i] = sum[i - 1] + cnt[i];
  }
  while (q--) {
    int t, l, r;
    cin >> t >> l >> r;
    l--;
    r--;
    long long ans = sum[r] - sum[l] + cnt[l];  // 它们儿子的和
    if (fa[l] == -1) {
      // 整个[1, n]的区间
      cout << ans + 1 << "\n";
    } else {
      // 计算它们之间的节点个数
      int L = lower_bound(edges[fa[l]].begin(), edges[fa[l]].end(), l) - edges[fa[l]].begin();
      int R = lower_bound(edges[fa[l]].begin(), edges[fa[l]].end(), r) - edges[fa[l]].begin() - 1;
      long long x = R - L + 1;
      ans += (long long) (1 + x) * x / 2;
      cout << ans << "\n";
    }
  }
  return 0;
}