该文章主要会写一些图形学相关内容。

将下图中v⃗\Large\vec{v}分解为n⃗\Large\vec{n}方向的投影a⃗\Large\vec{a}，以及垂直分量b⃗\Large\vec{b}。

01

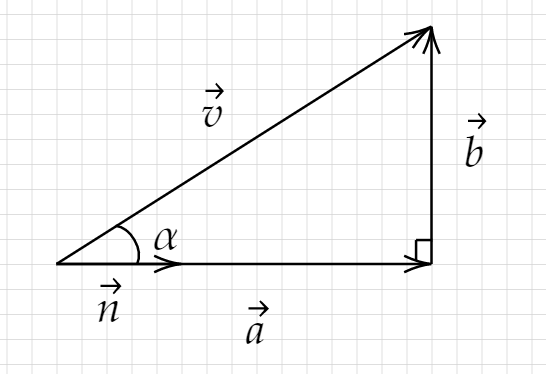
v⃗,e⃗,α\Large\vec{v},\vec{e},\alpha都是已知的量，

cos⁡α=∣a⃗∣∣v⃗∣\Large \cos{\alpha}=\frac{|\vec{a}|}{|\vec{v}|};

∣a⃗∣=∣v⃗∣cos⁡α\Large |\vec{a}|=|\vec{v}|\cos{\alpha};

a⃗=n⃗∣a⃗∣∣n⃗∣=n⃗∣v⃗∣cos⁡α∣n⃗∣=n⃗∣n⃗∣∣v⃗∣cos⁡α∣n⃗∣2=n⃗n⃗v⃗∣n⃗∣2\Large \vec{a}=\vec{n}\frac{|\vec{a}|}{|\vec{n}|}=\vec{n}\frac{|\vec{v}|\cos{\alpha}}{|\vec{n}|}=\vec{n}\frac{|\vec{n}||\vec{v}|\cos{\alpha}}{|\vec{n}|^2}=\vec{n}\frac{\vec{n}\vec{v}}{|\vec{n}|^2};

b⃗=v⃗−a⃗=v⃗−n⃗n⃗v⃗∣n⃗∣2\Large \vec{b}=\vec{v}-\vec{a}=\vec{v}-\vec{n}\frac{\vec{n}\vec{v}}{|\vec{n}|^2}.

向量叉积结果的模为两向量所组成的平行四边形面积。

02

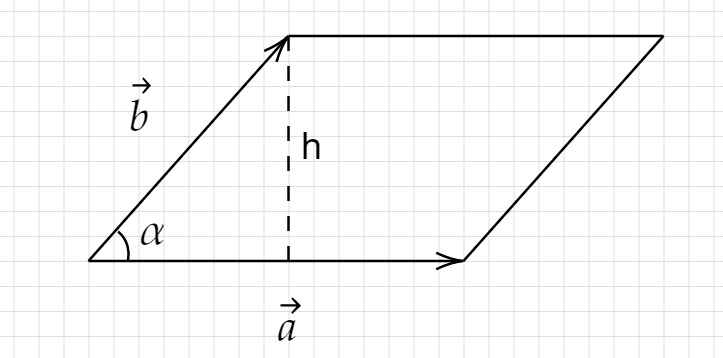
S=∣a⃗∣h\Large S=|\vec{a}|h;

sin⁡α=h∣b⃗∣\Large \sin{\alpha}=\frac{h}{|\vec{b}|};

h=∣b⃗∣sin⁡α\Large h=|\vec{b}|\sin{\alpha};

S=∣a⃗∣∣b⃗∣sin⁡α=∣a⃗×b⃗∣\Large S=|\vec{a}||\vec{b}|\sin{\alpha}=|\vec{a}\times\vec{b}|.

叉积判断二维两向量方向。

03

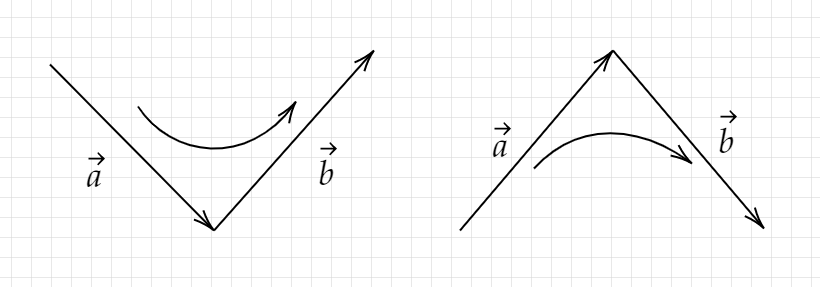
如果a⃗×b⃗>0\Large\vec{a}\times\vec{b}\gt0，则说明b⃗\Large\vec{b}在a⃗\Large\vec{a}的逆时针方向，即图中左边的情况。

否则如果a⃗×b⃗<0\Large\vec{a}\times\vec{b}\lt0，则说明b⃗\Large\vec{b}在a⃗\Large\vec{a}的顺时针方向，即图中右边的情况。

Andrew算法利用叉积求二维凸包。

首先将所有坐标按照xx轴为第一关键字，yy轴为第二关键字进行排序，分两次遍历所有点，分别求出上凸壳和下凸壳，利用单调栈维护点，以上求凸壳为例，如果栈顶的两个点和当前点的关系为上图中左边的情况，就将栈顶元素弹出，这样就使得栈中的元素按照顺序会始终“左拐”。